固定效应模型是什么?
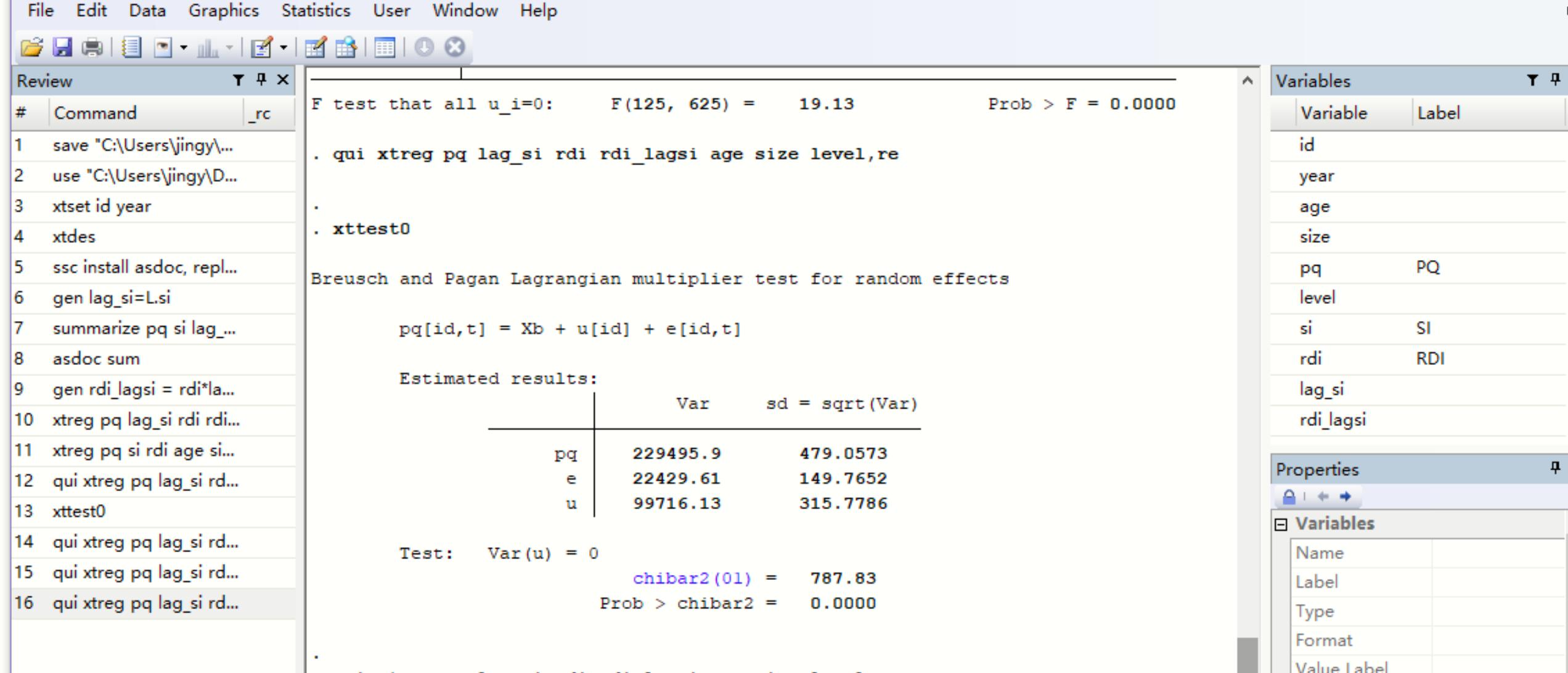
固定效应模型(Fixed Effects Model)是一种在面板数据分析中常用的方法,旨在控制个体间的异质性,从而更精准地估计解释变量对因变量的影响。想象一下,我们在研究多家公司的绩效与其研发投入、市场份额等因素的关系时,不同公司由于各自独特的企业文化、管理模式、地理位置等因素,即使在相同的解释变量水平下,绩效也可能存在显著差异。这些公司特有的、不随时间变化的因素就是个体异质性。如果不加以控制,它们可能会干扰我们对研发投入、市场份额等解释变量与绩效之间真实关系的判断。固定效应模型的巧妙之处在于,它通过引入一系列虚拟变量作为固定效应,来捕捉这些个体间的差异。例如,在研究中加入行业固定效应,就是为了控制不同行业之间的系统性差异,如制造业与服务业在生产流程、市场竞争模式等方面的固有区别;加入年份固定效应,则可以控制宏观经济环境、政策法规等随时间变化但对所有个体产生共同影响的因素,像经济繁荣期与衰退期对各行业企业的不同冲击。
固定效应模型的 Stata 命令
在 Stata 中,实现固定效应模型有多种方法,下面为大家介绍几种常用的命令:
LSDV 法
通过在回归方程中以 “i.” 形式加入虚拟变量来代表不同的个体或时间等因素,从而实现固定效应的控制。例如,如果我们有个体层面的固定效应,且个体变量为 “id”,时间变量为 “year”,在控制其他解释变量 “x” 和 “controls” 对因变量 “y” 的影响时,命令可以写成:这里的 “cluster (stkcd)” 是为了处理可能存在的聚类效应,以获得更稳健的标准误估计。如果模型仅存在个体效应,可写为:若仅存在时间效应,则是:需要注意的是,当个体数量较多时,使用 LSDV 法会生成大量虚拟变量,可能导致自由度损失过多,甚至超出 Stata 允许的解释变量个数,还会增加运行时间和结果的复杂性,而且可能存在多重共线性问题,需要谨慎处理。
组内估计法
首先使用 “xtset” 命令设定面板数据,明确截面(个体)维度和时间维度。假设我们的截面变量是 “industry”,时间变量是 “year”,对于个体固定效应模型,命令如下:其中 “fe” 代表固定效应模型,“robust” 表示采用稳健标准误,以应对数据中可能存在的异方差等问题,提高估计的可靠性。如果要控制时间固定效应,可以这样写:而对于双向固定效应模型(同时控制个体和时间固定效应),命令为:组内估计法得到的系数是较为纯正的固定效应估计量,但在使用 “xtreg” 命令前一定要正确设定面板数据,否则可能得到错误的结果。
其他方法
除了上述两种常见方法外,还有 “areg”“reghdfe” 等方法。“areg” 命令在处理固定效应时也有其独特的应用场景,例如在某些情况下可以通过 “absorb” 选项来控制固定效应,其语法相对简洁。“reghdfe” 则是一个功能强大的命令,特别适用于处理多维固定效应的情况。当我们需要同时控制多个维度的固定效应,如城市、行业、年度等,使用 “reghdfe” 可以大大提高计算效率,避免因使用过多虚拟变量导致的问题。例如:这里 “id” 和 “year” 分别代表个体和时间维度的固定效应,“reghdfe” 会自动处理这些固定效应,得到准确且高效的估计结果,在处理大规模面板数据和复杂固定效应结构时表现出色。
固定效应模型选择与检验
F 检验
在确定是否使用固定效应模型时,F 检验是一种常用的方法。F 检验的原假设是个体效应或时间效应等因素不存在,即固定效应模型并不比混合 OLS(普通最小二乘法)模型更优。通过检验,我们可以判断是否应该引入固定效应来控制个体间的异质性。对于单因素效应(如个体固定效应或时间固定效应),在 Stata 输出的固定效应模型结果中,会直接给出 F 值和相应的 P 值。如果 P 值小于设定的显著性水平(通常为 0.05),则拒绝原假设,这意味着固定效应模型相较于混合 OLS 模型更能解释数据的变化,此时采用固定效应模型更为合适。例如,在研究企业生产效率与企业规模、技术投入等因素的关系时,若个体固定效应的 F 检验 P 值显著,就表明不同企业之间存在显著的个体异质性,需要通过固定效应模型来控制这些差异,以准确估计技术投入等变量对生产效率的影响。而对于双向效应(如同时存在个体和时间固定效应)的情况,情况会稍微复杂一些。此时,模型结果中的 F 检验 P 值仅能用于判断是否存在个体效应。若要全面判断双向效应的显著性,需要进一步结合其他方法或进行额外的检验,如联合显著性检验等,以确定时间效应和个体效应是否同时显著,从而判断双向固定效应模型的适用性。
豪斯曼检验
豪斯曼检验(Hausman Test)主要用于在固定效应模型和随机效应模型之间做出选择。其核心思想是比较这两种模型估计量的差异是否显著。随机效应模型假设个体效应是随机分布的,并且与解释变量不相关;而固定效应模型则将个体效应视为固定的、待估计的参数。豪斯曼检验的原假设是随机效应模型是合适的,即个体效应与解释变量不相关。在 Stata 中,首先需要分别估计固定效应模型和随机效应模型,然后使用 “hausman” 命令进行检验。例如,在研究居民消费行为与收入、利率等因素的关系时,先运行 “xtreg” 命令分别以 “fe” 和 “re” 选项估计固定效应模型和随机效应模型,并将结果存储起来,接着使用 “hausman” 命令比较这两个模型的估计结果。如果豪斯曼检验的结果拒绝原假设(通常以 P 值小于 0.05 或其他设定的显著性水平为判断标准),则说明固定效应模型和随机效应模型的估计量存在显著差异,此时应选择固定效应模型,因为固定效应模型能够更有效地控制个体异质性,得到更可靠的估计结果;反之,如果不拒绝原假设,则可以考虑使用随机效应模型,尤其是在样本量较大且个体效应的方差较小的情况下,随机效应模型可能具有更高的估计效率。
实例演示
为了让大家更直观地了解固定效应模型在 Stata 中的应用,我们以一个具体的研究案例为例。假设我们要研究不同企业的生产效率与企业规模、技术投入、管理水平以及所在地区和年份的关系。我们收集了 50 家企业在 2010 - 2020 年的数据,数据集中包含以下变量:因变量:生产效率(efficiency)自变量:企业规模(scale)、技术投入(tech)、管理水平(manage)固定效应变量:企业个体(id)、年份(year)控制变量:行业类型(industry)首先,我们将数据导入 Stata 中,使用 “use” 命令,假设数据文件名为 “production.dta”,命令如下:接着,使用 “xtset” 命令声明面板数据结构,明确截面变量为企业个体 “id”,时间变量为 “year”:然后,我们可以使用 “xtreg” 命令来估计双向固定效应模型,控制企业个体和年份的固定效应,同时纳入其他解释变量和控制变量:在 Stata 输出的结果中,我们可以看到各个自变量的回归系数、标准误、t 值和 p 值等信息。例如,企业规模的系数为 0.25,标准误为 0.05,t 值为 5.00,p 值为 0.000,这表明在控制了企业个体和年份的固定效应以及其他因素后,企业规模每增加一个单位,生产效率平均提高 0.25 个单位,且该影响在统计上是显著的。同时,结果中还会给出固定效应的估计值,如各个企业个体的固定效应系数和年份的固定效应系数。这些系数可以帮助我们了解不同企业和不同年份对生产效率的特定影响。此外,我们还可以通过 F 检验和豪斯曼检验来进一步验证固定效应模型的适用性和合理性。如果 F 检验的 p 值小于 0.05,说明固定效应模型比混合 OLS 模型更能解释数据的变化;如果豪斯曼检验的 p 值小于 0.05,则表明固定效应模型优于随机效应模型,我们选择固定效应模型是合理的。通过这个实例,我们可以看到固定效应模型在 Stata 中的实际应用过程,以及如何解读和分析模型的结果,从而为我们的研究提供有力的支持和依据。在实际研究中,大家可以根据自己的数据和研究问题,灵活运用固定效应模型和相应的 Stata 命令,深入挖掘数据背后的信息和规律。
总结
固定效应模型在面板数据分析中占据着重要地位,它为我们提供了一种有效的方式来控制个体间的异质性,从而更准确地揭示变量之间的关系。通过本文介绍的多种 Stata 命令,如 LSDV 法、组内估计法以及 “areg”“reghdfe” 等方法,研究者可以根据数据的特点和研究问题的需求,灵活选择合适的估计方法。同时,F 检验和豪斯曼检验等方法能够帮助我们在不同的模型设定中做出明智的选择,确保模型的合理性和可靠性。在实际应用中,我们需要深入理解固定效应模型的原理和假设,正确运用 Stata 命令,并结合实际问题进行合理的模型设定和结果解读。只有这样,我们才能充分发挥固定效应模型的优势,从复杂的数据中提取出有价值的信息,为学术研究和实际决策提供有力的支持。希望本文能够帮助大家更好地掌握固定效应模型及其 Stata 应用,在数据分析的道路上不断探索前行,取得更多有意义的研究成果。

